다익스트라(Dijkstra)
다익스트라 알고리즘이란?
- 한 정점에서 다른 모든 정점으로의 최단 경로를 찾는 알고리즘이다.
- 가중치가 양수인 경우에만 사용할 수 있다.
- 가중치 중 음수가 존재하지 않기 때문에 그래프에 있는 모든 간선을 단 한 번만 처리한다.
- 우선순위큐를 이용하여 효율적으로 구현할 수 있다.
다익스트라 실행 과정
- 1. 모든 정점의 거리값을 무한으로 설정한다.(시작점의 거리값은 0)
- 2. 시작 노드와 인접한 노드들의 거리값을 설정한다.
시작 노드의 거리값 + 인접한 노드까지의 가중치 < 인접한 노드의 거리값 인 경우 인접한 노드의 거리값을 갱신한다.
인접한 노드의 거리값이 갱신된 경우 해당 노드를 우선순위큐에 넣는다.
- 3. 우선순위 큐의 루트 노드를 선택하고, 해당 노드가 방문하지 않은 노드인 경우 해당 노드의 인접한 노드를 살펴본다.
- 4. 모든 정점을 탐색하면 종료한다.



- A노드의 거리값(0) + A-B의 가중치(3) < B노드의 거리값(무한대)이 성립하기 때문에 B노드의 거리값을 3으로 갱신.
- A노드의 거리값(0) + A-C의 가중치(6) < C노드의 거리값(무한대)이 성립하기 때문에 C노드의 거리값을 6으로 갱신.

- A노드는 이미 방문했기 때문에 갱신 과정을 생략한다.
- B노드의 거리값(3) + B-D의 가중치(7) < D노드의 거리값(무한대)이 성립하기 때문에 D노드의 거리값을 10으로 갱신.
- B노드의 거리값(3) + B-E의 가중치(7) < E노드의 거리값(무한대)이 성립하기 때문에 E노드의 거리값을 10으로 갱신.
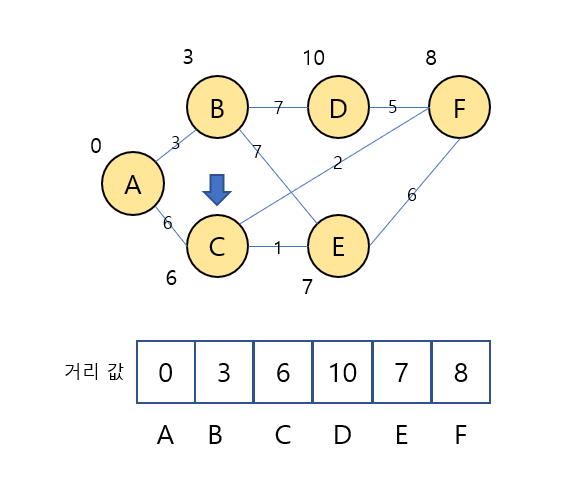
- A노드는 이미 방문했기 때문에 갱신 과정을 생략한다.
- C노드의 거리값(6) + C-E의 가중치(1) < E노드의 거리값(10)이 성립하기 때문에 E노드의 거리값을 7로 갱신.
- C노드의 거리값(6) + C-F의 가중치(2) < F노드의 거리값(무한대) 가 성립하기 때문에 F노드의 거리값을 8로 갱신.

- C노드는 이미 방문했기 때문에 갱신 과정을 생략한다.
- E노드의 거리값(7) + E-F의 가중치(6) < F노드의 거리값(8)이 성립하지 않기 때문에 F노드의 거리값을 갱신하지 않는다.
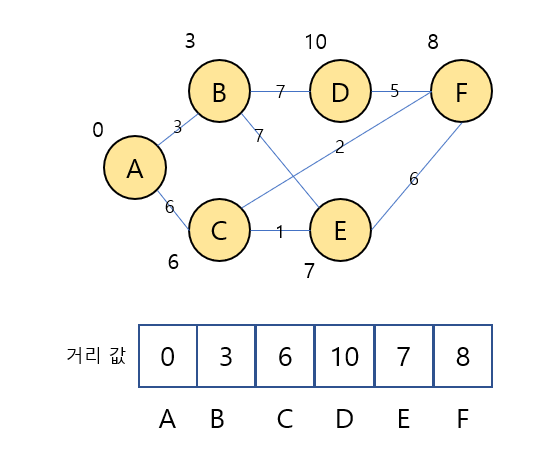
* 우선순위 큐에는 노드의 거리값이 갱신될 경우 넣는다.
* 우선순위 큐의 루트 노드를 기준으로 탐색할 노드를 결정한다.
다익스트라 코드(C++)
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
vector<int> dijkstra(vector<vector<pair<int, int>>> &g,int start)
{
priority_queue<pair<int, int>> pq;
vector<int> dist(6,INT_MAX);
dist[start] = 0;
bool visit[6]={0,};
visit[start]=true;
pq.push(make_pair(0, start));
while (!pq.empty())
{
int nowCost = -pq.top().first;
int nowNode = pq.top().second;
pq.pop();
if(visite[nowNode])
continue;
visit[nowNode] = true;
for (auto nextPair : g[nowNode])
{
int nextNode = nextPair.first;
int nextCost = nextPair.second;
if(visit[nextNode])
continue;
if (dist[nextNode] > dist[nowNode] + nextCost)
{
dist[nextNode] = dist[nowNode] + nextCost;
// 우선순위큐는 기본 값이 maxHeap이기 때문에 거리값의
// 절대값이 작은 수 부터 탐색하기 위해 -를 붙인다.
pq.push(make_pair(-dist[nextNode], nextNode));
}
}
}
return dist;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
// 노드,가중치
vector<vector<pair<int,int>>> g={
{make_pair(1,3),make_pair(2,6) },
{ make_pair(0,3),make_pair(3,7),make_pair(4,7) },
{ make_pair(0,6),make_pair(4,1),make_pair(5,2) },
{ make_pair(1,7),make_pair(5,5) },
{ make_pair(1,7),make_pair(2,1),make_pair(5,6) },
{ make_pair(2,2),make_pair(3,5),make_pair(4,6) }
};
vector<int> dist = dijkstra(g,0);
for (int i = 0; i < dist.size(); i++)
{
cout << "0부터 " << i << "까지의 거리 : " << dist[i] << endl;
}
return 0;
}

'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| 최단 경로 알고리즘 - 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2020.11.23 |
|---|---|
| 최단 거리 알고리즘 - 벨만-포드(Bellman-Ford) 알고리즘 (0) | 2020.11.23 |
| 탐색 알고리즘 - 너비 우선 탐색(Breadth First Search, BFS) (0) | 2020.06.22 |
| 탐색 알고리즘 - 깊이 우선 탐색(Depth First Search, DFS) (0) | 2020.06.22 |
| 탐색 알고리즘 - 이분 탐색(Binary Search) (0) | 2020.06.22 |




댓글